Trigonometry
Prerequisites:
- Nothing
All you've learned so far has been easy, but from here on, we'll be working on what's called AC. AC (Alternating) is basically a sine voltage. If you know what that means, you can skip this tutorial, but for those who don't, stick around for this short primer on trigonometry.
Let's get started.
Let's get started.
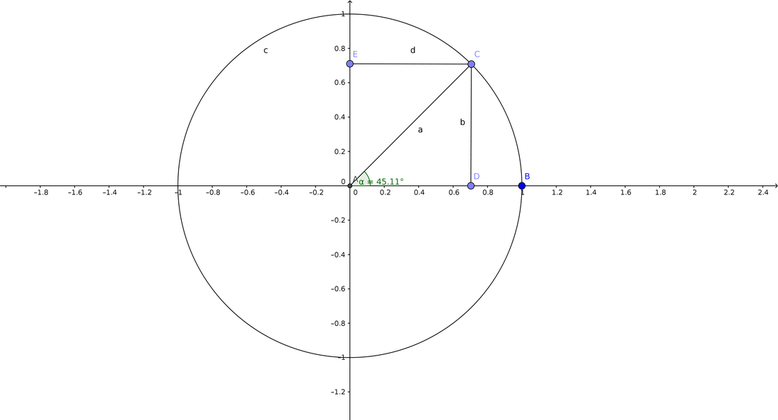
What you're seeing above is quite "scary", but that's only it's appearance. The circle you're seeing above is what's called a "unit" circle - a fancy term meaning a circle of radius 1. Let's say we take any radius, and then rotate it around the center of the circle. Then we imagine a line perpendicular to the point from the x and y axes, you get two very special ratios, and consequently one of the most used ones as well -
$$\sin{\alpha}$$
$$\cos{\alpha}$$
where $\alpha$ is simply the angle between the x axis and the radius we're turning.
To be exact, $\sin{\alpha}$ is defined as the ratio of the side opposite to $\alpha$ and the hypotenuse of the right triangle in which the angle is formed. And $\cos{\alpha}$ follows suit, but the opposite side is replaced with the adjacent side-
$$\sin{\alpha} = \frac{b}{a}$$
$$ a = 1, so$$
$$\sin{\alpha} = b$$
$$\cos{\alpha} = \frac{d}{a}$$
$$ a = 1, so$$
$$\cos{\alpha} = d$$
There are a few other ratios as well, and I'll define them below -
$$\tan{\alpha} = \frac{\sin{\alpha}}{\cos{\alpha}}$$
$$cosec{\alpha} = \frac{1}{\sin{\alpha}}$$
$$\sec{\alpha} = \frac{1}{\cos{\alpha}}$$
$$\cot{\alpha} = \frac{1}{\tan{\alpha}}$$
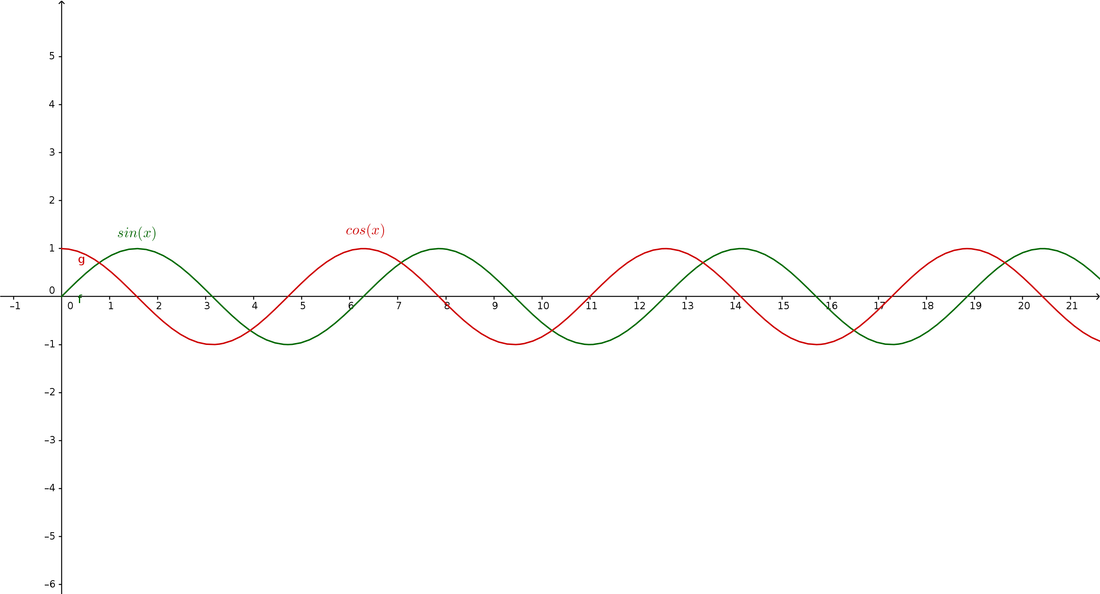
And the math's over. But a bit of visual "help" is still needed to understand trigonometry
$$\sin{\alpha}$$
$$\cos{\alpha}$$
where $\alpha$ is simply the angle between the x axis and the radius we're turning.
To be exact, $\sin{\alpha}$ is defined as the ratio of the side opposite to $\alpha$ and the hypotenuse of the right triangle in which the angle is formed. And $\cos{\alpha}$ follows suit, but the opposite side is replaced with the adjacent side-
$$\sin{\alpha} = \frac{b}{a}$$
$$ a = 1, so$$
$$\sin{\alpha} = b$$
$$\cos{\alpha} = \frac{d}{a}$$
$$ a = 1, so$$
$$\cos{\alpha} = d$$
There are a few other ratios as well, and I'll define them below -
$$\tan{\alpha} = \frac{\sin{\alpha}}{\cos{\alpha}}$$
$$cosec{\alpha} = \frac{1}{\sin{\alpha}}$$
$$\sec{\alpha} = \frac{1}{\cos{\alpha}}$$
$$\cot{\alpha} = \frac{1}{\tan{\alpha}}$$
And the math's over. But a bit of visual "help" is still needed to understand trigonometry