Thevenin Equivalent Circuit
Prerequisites:
- Knowledge about resistors, Ohm's Law, KVL and KCL (Kirchoff's Voltage and Current Laws)
As you start making projects, you'll find that your resistor networks are becoming huge and unwieldy. Also, you'll find out that you'll need to do tons of math. There's something called the Thevenin Equivalent Circuit that simplifies it into a single voltage source and a resistor. Sounds great? It is, and it's really easy as well. Also, this is very useful in circuit analysis as well. You'll be soon working on projects that involve many resistors, and other components, and simplyfying resisor networks can prove to be a huge help. Let's get started.
Let's say there's a resistor circuit, and you've got two points of interest, where you want to simplfy the circuit, you measure the voltage as it is, and then you short the two points and find the current, then you divide the voltage by the current, so you get the resistance. The voltage and resistance you've found is often called the thevenin equivalent voltage and resistance, and the whole circuit is named the same as this article's title.and you can kinda substitue that circuit into the rest of the circuit. The in-Practice section should help you.
Let's say there's a resistor circuit, and you've got two points of interest, where you want to simplfy the circuit, you measure the voltage as it is, and then you short the two points and find the current, then you divide the voltage by the current, so you get the resistance. The voltage and resistance you've found is often called the thevenin equivalent voltage and resistance, and the whole circuit is named the same as this article's title.and you can kinda substitue that circuit into the rest of the circuit. The in-Practice section should help you.
In Practice
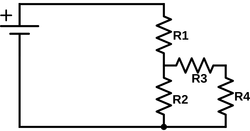
Let's go back to a modified version of the last tutorial's voltage divider:
|
It's a simple circuit to calculate without any simplifications, but it's also great to show how to use the technique of thevenin equivalent circuits. Now, ignore $R_3$ and $R_4$ (since we need the open circuit voltage), and find the Voltage across the 2 points, which we previously calculated to be:
$$V_{in}\times\left(\frac{R_2}{\left(R_1 + R_2\right)}\right)$$
which equals $V_{th}$ (short for Voltage thevenin)
Now, short the 2 points. Since the voltage across $R_2$ is the same, $V_d$ is $0$ (since the voltage on an ideal wire is the same everywhere),
so the current
$$I_{th} = \frac{V_{in}}{R_1}$$
Which means that the thevenin resistance
$$R_{th} = \frac{V_{th}}{I_{th}} = V_{in} \times \frac{\left(\frac{R_2}{\left(R_1 + R_2\right)}\right)}{\left(\frac{V_{in}}{R_1}\right)} = \frac{\left(R_1 \times R_2\right)}{\left(R_1 + R_2\right)}$$
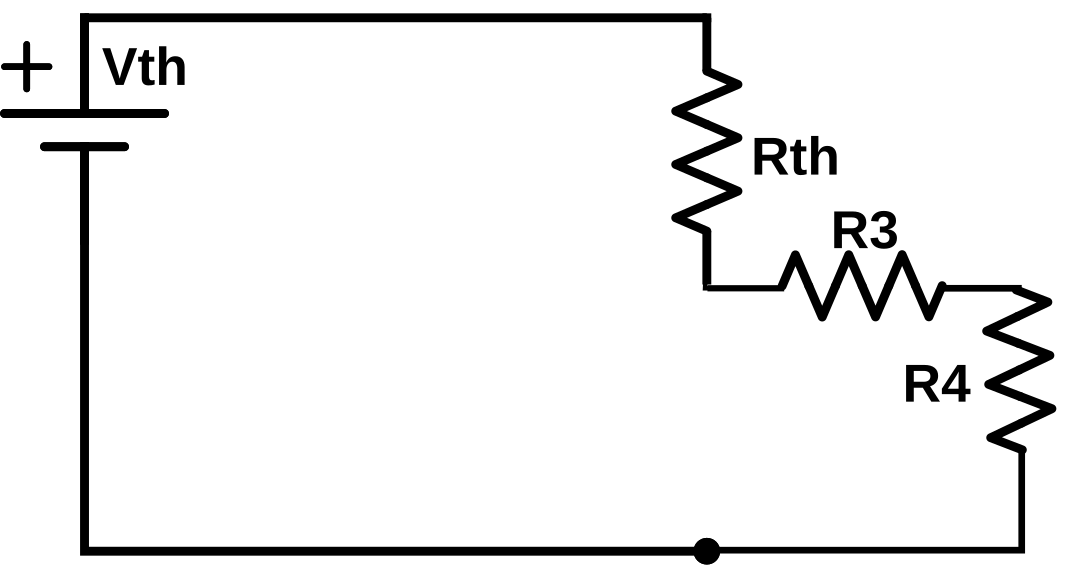
so the new circuit now is:
$$V_{in}\times\left(\frac{R_2}{\left(R_1 + R_2\right)}\right)$$
which equals $V_{th}$ (short for Voltage thevenin)
Now, short the 2 points. Since the voltage across $R_2$ is the same, $V_d$ is $0$ (since the voltage on an ideal wire is the same everywhere),
so the current
$$I_{th} = \frac{V_{in}}{R_1}$$
Which means that the thevenin resistance
$$R_{th} = \frac{V_{th}}{I_{th}} = V_{in} \times \frac{\left(\frac{R_2}{\left(R_1 + R_2\right)}\right)}{\left(\frac{V_{in}}{R_1}\right)} = \frac{\left(R_1 \times R_2\right)}{\left(R_1 + R_2\right)}$$
so the new circuit now is:
A circuit that's much easier to analyze, since you simply add resistances in series (you can confirm using KVL and KCL)
|
