The Inductor
Prerequisites:
- All previous tutorials except for the Complex Numbers
The inductor - woooooooo, maghnetism all kinds of voodoo magic....
That was a bad joke, but that aside, if you're a hobbyist, you must have heard of "The Inductor" which is so magical and all kinds of stuff and complicated, but what are they??
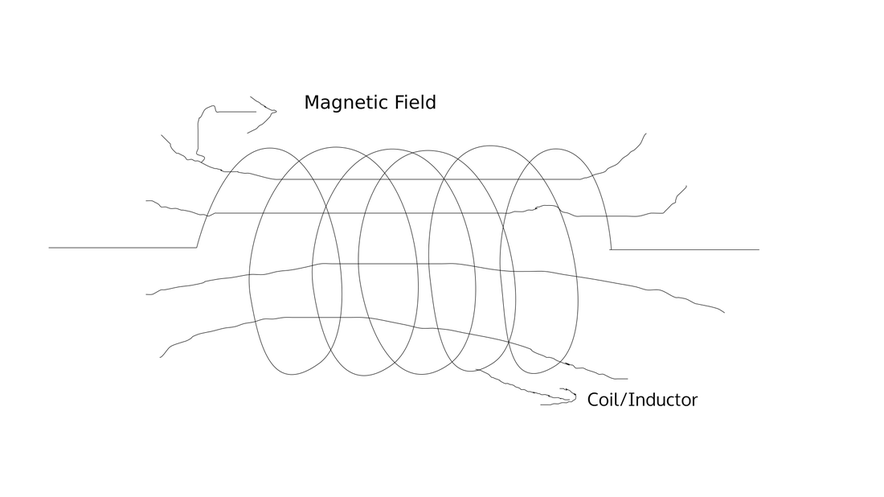
They are, wait for it- a simple coil of wire.
That's it? Yeah, that's totally it.
In fact, every single loop of circuit you've ever made wll act as an inductor, since you have a "one turn" coil of wire. And yes this also applies to capacitors, every single circuit you make will have (parasitic) resistance, capacitance and inductance, and you shouldn't care about that for the most part, except in really special situations, but back on track-
What's so great about them?? Every single nerd and geek has played with the "electromagnet" experiment, you make a coil of wire, pass a current through it, and voila, a magnet, it's similar, but the other way around, When a steady current passes through a loop of wire, a magnetic field builds around the loop, and when the current changes, it tries to maintain the original current as the changing magnetic field induces a current (when you have a changing magnetic field near a coil, it'll induce a current in it, this btw, is also how generators produce electricity).
So, basic rule, similar to capacitors, it tries to maintain something stable, in this case current unlike voltage for capacitors.
That was a bad joke, but that aside, if you're a hobbyist, you must have heard of "The Inductor" which is so magical and all kinds of stuff and complicated, but what are they??
They are, wait for it- a simple coil of wire.
That's it? Yeah, that's totally it.
In fact, every single loop of circuit you've ever made wll act as an inductor, since you have a "one turn" coil of wire. And yes this also applies to capacitors, every single circuit you make will have (parasitic) resistance, capacitance and inductance, and you shouldn't care about that for the most part, except in really special situations, but back on track-
What's so great about them?? Every single nerd and geek has played with the "electromagnet" experiment, you make a coil of wire, pass a current through it, and voila, a magnet, it's similar, but the other way around, When a steady current passes through a loop of wire, a magnetic field builds around the loop, and when the current changes, it tries to maintain the original current as the changing magnetic field induces a current (when you have a changing magnetic field near a coil, it'll induce a current in it, this btw, is also how generators produce electricity).
So, basic rule, similar to capacitors, it tries to maintain something stable, in this case current unlike voltage for capacitors.
Now, if you'll excuse my bad digital drawing skills (what was I supposed to do? I DO NOT HAVE A GRAPHIC TABLET, so cut me some slack wouldya....).
Let's get introduce to some equations-
$$V = L\frac{dI}{dT}$$
Where $L = \frac{{\mu}N^2A}{L}$, $N$ is the number of turns and $A$ is the area, while $L$ is the lengh of the inductor (NOT THE WIRE). As for ${\mu}$, it's the "permeability", a constant that depends on the medium, usually air or a ferrite core.
You'll see a few similarities to the Capacitor's equation, but the roles are reversed. If you have a steady amount of current flowing through an inductor, the voltage drop across it will be huge, since the current going through it will change in a very short amount of time. This is also the reason you'll often see diodes around inductors and transformers, so that the high voltage (~10000V even for small ones) is clamped. But what's so awesome about these?
Well, they aren't that useful in DC applications, but they're REALLY useful with AC or rather any kindof variable voltage signal. But we'll come to that later on when we learn about complex impedances.
But for now, you can go with one really simple application- Transformers. They only work with AC voltages, and the changing voltage causes a changing magnetic field, which induces another inductor nearby. The ratio of the voltages are simply ratio of the number of turns (around the same core).
This might have been a disappointing tutorial, but really there's not much to learn about inductors themselves as indepedent components. But they do get quite useful when used with other components
Let's get introduce to some equations-
$$V = L\frac{dI}{dT}$$
Where $L = \frac{{\mu}N^2A}{L}$, $N$ is the number of turns and $A$ is the area, while $L$ is the lengh of the inductor (NOT THE WIRE). As for ${\mu}$, it's the "permeability", a constant that depends on the medium, usually air or a ferrite core.
You'll see a few similarities to the Capacitor's equation, but the roles are reversed. If you have a steady amount of current flowing through an inductor, the voltage drop across it will be huge, since the current going through it will change in a very short amount of time. This is also the reason you'll often see diodes around inductors and transformers, so that the high voltage (~10000V even for small ones) is clamped. But what's so awesome about these?
Well, they aren't that useful in DC applications, but they're REALLY useful with AC or rather any kindof variable voltage signal. But we'll come to that later on when we learn about complex impedances.
But for now, you can go with one really simple application- Transformers. They only work with AC voltages, and the changing voltage causes a changing magnetic field, which induces another inductor nearby. The ratio of the voltages are simply ratio of the number of turns (around the same core).
This might have been a disappointing tutorial, but really there's not much to learn about inductors themselves as indepedent components. But they do get quite useful when used with other components