AC Current, Complex impedances, Voltages And Currents
Prerequisites:
- All the previous tutorials
- Time. This one is going to be LONG
AC Current:
AC Current, the thing I've waited so long to teach you, is one of the best things ever. This is going to form the basis of literally every analog circuit you'll ever build, so listen up people.
I'm pretty sure that by now, unless you were living under a rock (I'm not judging, but the rock must have been really comfortable), you know that AC stands for Alternating Current. What is it actually then? Well, literally what it means. It represents Voltage that changes with time. Every signal we studied last time around is an AC signal, but when we're working with circuits, we usually consider a sine voltage, because of the fact that it can be extended easily to the other waves thanks to Fourier theorem. For now, when speaking generally, we'll take AC to mean a sinusoidal voltage. When we talk about the frequency (Oh, BTW, remember this formula - $\omega = 2\pi f$, where $\omega$ is the angular frequency of the wave, and f is the frequency), we mean the frequency of the sine wave. This applies for all the properties of the AC Voltage.
Impedances:
We all know about resistances. They're simple to deal with, after all. You have Ohm's law, which is one of the simplest thing evah. But they are only about resistors (not quite, they're only about anything with a time independent value of $\frac{V}{I}$, which basically mean, for any voltage, the current shouldn't change regardless of time as long as the voltage remains constant, this also means $R$ is independent of time, but not necessarily of voltage and therefore current), then what about capacitors and inductor? Their currents change with time for a constant voltage. Well, these components, quite frankly have no business with any kind of DC circuits (except for filtering, we'll come to that later), then what about AC voltages? Well, let's find out.
It's a go time. (Yes, I like Mario, come bite me)
Let's start with Capacitors.
You guys remember the formula, right? (please tell me you do, please)
$$i = C\frac{dV_C}{dt}$$
Well, we know that an AC Voltage is sinusoidal, so
$$V_C = V_0sin(\omega t)$$
Differentiating that with respect to time (don't worry if you don't know calculus, skip the calculations and understand the result. I still recommend you to learn a bit about calculus, nothing too deep, just elementary differentiation and integration, trust me, it takes you a long way), we get
$$\frac{dV_C}{dt} = V_0\omega cos(\omega t)$$
Which means,
$$C\frac{dV_C}{dt} = i = CV_0\omega cos(\omega t)$$
What does that mean? Not much really. It basically says that the current will always be $\frac{\pi}{2}$ radians ahead of the voltage. So, you could sum up the current as -
$$i = constant \times V_0 sin(\omega t + \frac{\pi}{2})$$
That's all fine, but the "resistance", if we define one, is well, dependent on time. That's obvious. But if we confine ourselves to AC only situations, we can simply throw away the information about the phase (the $sin$ and $cos$ part), and just compare the amplitudes, which is a pretty good way to measure the "resistance". This is what we call reactance (or more generally impedance. When you say reactance, you only have reactive components (caps and inductors) in mind, but when you say impedance, it can mean a resistor can be in the mix too, although, they are interchanged quite often, as it's not hard to understand what the other guy has in mind). All that talk aside, we can define the capacitive reactance (denoted by symbol $X_c$) as -
$$X_c = \frac{|V_C|}{|i|} = \frac{V_0}{V_0\omega C} = \frac{1}{\omega C}$$ The symbol $|x|$ basically means the amplitude of $x$, nothing more.
Remember that equation. It's basically Ohm's law for Capacitors. And it's pretty damn useful. When building simple circuits, you don't really care about the phase as much as you do about the amplitudes (why the hell would anyone be concerned with the phase information of a guitar amp? The amplitudes are important though, for dat bass). But you should see one peculiar thing there - it depends on the angular frequency and thus, the frequency. It's simple to see that the reactance drops to 0 as $\omega$ becomes larger and the opposite is true as well, like come on. why wouldn't it be? But that gives us a good view on how the capacitor is useful - it's basically a short for higher frequencies, but it's pretty much open for the lower ones. It's useful to seperate a mix of low and high frequencies (We'll see more of that below). But that's the complete theory of the capacitor that I intend to teach you. Let's shift our focus - the Inductor.
I'll keep this pretty short, since I'll be doing almost exactly what I did in the previous section -
$$V_l = L\frac{di}{dt}$$
Let's assume here that $i = i_0sin(\omega t)$
$$V_l = L\frac{d(i_0sin(\omega t)}{dt} = L \dot i_0\omega cos(\omega t)$$
The inductive reactance $X_l$ is -
$$X_l = \frac{|V_l|}{|i|} = \omega L$$
Two things should be noted here,
1. The current is $\frac{\pi}{2}$ behind.
2. The expression for $X_l$ means that an inductor behave exactly like the capacitor, just in reverse. It will block high frequency signals and allows low frequency ones. This makes it useful for noise removal (it's usually done with caps though).
And that's all there is to impedances. One thing to keep in mind is that impedances behave exactly like resistances during calculations. They add together in series, and when parallel, the inverse is equal to the sum of the inverses of every individual impedance. But as I've mentioned before, the impedance will change with the frequency, making it extremely useful. In fact, this property is exactly what lets us use Radios and other wireless forms of communications, but that's FAR down the lane. But for now, impedances are over. I'll recommend a pizza, or maybe go watch a new episode of Shingeki no Kyojin or Boku no Hero Academia, have a bit of fun. This was a lot of work, but it's gonna get much better now onwards.
AC Current, the thing I've waited so long to teach you, is one of the best things ever. This is going to form the basis of literally every analog circuit you'll ever build, so listen up people.
I'm pretty sure that by now, unless you were living under a rock (I'm not judging, but the rock must have been really comfortable), you know that AC stands for Alternating Current. What is it actually then? Well, literally what it means. It represents Voltage that changes with time. Every signal we studied last time around is an AC signal, but when we're working with circuits, we usually consider a sine voltage, because of the fact that it can be extended easily to the other waves thanks to Fourier theorem. For now, when speaking generally, we'll take AC to mean a sinusoidal voltage. When we talk about the frequency (Oh, BTW, remember this formula - $\omega = 2\pi f$, where $\omega$ is the angular frequency of the wave, and f is the frequency), we mean the frequency of the sine wave. This applies for all the properties of the AC Voltage.
Impedances:
We all know about resistances. They're simple to deal with, after all. You have Ohm's law, which is one of the simplest thing evah. But they are only about resistors (not quite, they're only about anything with a time independent value of $\frac{V}{I}$, which basically mean, for any voltage, the current shouldn't change regardless of time as long as the voltage remains constant, this also means $R$ is independent of time, but not necessarily of voltage and therefore current), then what about capacitors and inductor? Their currents change with time for a constant voltage. Well, these components, quite frankly have no business with any kind of DC circuits (except for filtering, we'll come to that later), then what about AC voltages? Well, let's find out.
It's a go time. (Yes, I like Mario, come bite me)
Let's start with Capacitors.
You guys remember the formula, right? (please tell me you do, please)
$$i = C\frac{dV_C}{dt}$$
Well, we know that an AC Voltage is sinusoidal, so
$$V_C = V_0sin(\omega t)$$
Differentiating that with respect to time (don't worry if you don't know calculus, skip the calculations and understand the result. I still recommend you to learn a bit about calculus, nothing too deep, just elementary differentiation and integration, trust me, it takes you a long way), we get
$$\frac{dV_C}{dt} = V_0\omega cos(\omega t)$$
Which means,
$$C\frac{dV_C}{dt} = i = CV_0\omega cos(\omega t)$$
What does that mean? Not much really. It basically says that the current will always be $\frac{\pi}{2}$ radians ahead of the voltage. So, you could sum up the current as -
$$i = constant \times V_0 sin(\omega t + \frac{\pi}{2})$$
That's all fine, but the "resistance", if we define one, is well, dependent on time. That's obvious. But if we confine ourselves to AC only situations, we can simply throw away the information about the phase (the $sin$ and $cos$ part), and just compare the amplitudes, which is a pretty good way to measure the "resistance". This is what we call reactance (or more generally impedance. When you say reactance, you only have reactive components (caps and inductors) in mind, but when you say impedance, it can mean a resistor can be in the mix too, although, they are interchanged quite often, as it's not hard to understand what the other guy has in mind). All that talk aside, we can define the capacitive reactance (denoted by symbol $X_c$) as -
$$X_c = \frac{|V_C|}{|i|} = \frac{V_0}{V_0\omega C} = \frac{1}{\omega C}$$ The symbol $|x|$ basically means the amplitude of $x$, nothing more.
Remember that equation. It's basically Ohm's law for Capacitors. And it's pretty damn useful. When building simple circuits, you don't really care about the phase as much as you do about the amplitudes (why the hell would anyone be concerned with the phase information of a guitar amp? The amplitudes are important though, for dat bass). But you should see one peculiar thing there - it depends on the angular frequency and thus, the frequency. It's simple to see that the reactance drops to 0 as $\omega$ becomes larger and the opposite is true as well, like come on. why wouldn't it be? But that gives us a good view on how the capacitor is useful - it's basically a short for higher frequencies, but it's pretty much open for the lower ones. It's useful to seperate a mix of low and high frequencies (We'll see more of that below). But that's the complete theory of the capacitor that I intend to teach you. Let's shift our focus - the Inductor.
I'll keep this pretty short, since I'll be doing almost exactly what I did in the previous section -
$$V_l = L\frac{di}{dt}$$
Let's assume here that $i = i_0sin(\omega t)$
$$V_l = L\frac{d(i_0sin(\omega t)}{dt} = L \dot i_0\omega cos(\omega t)$$
The inductive reactance $X_l$ is -
$$X_l = \frac{|V_l|}{|i|} = \omega L$$
Two things should be noted here,
1. The current is $\frac{\pi}{2}$ behind.
2. The expression for $X_l$ means that an inductor behave exactly like the capacitor, just in reverse. It will block high frequency signals and allows low frequency ones. This makes it useful for noise removal (it's usually done with caps though).
And that's all there is to impedances. One thing to keep in mind is that impedances behave exactly like resistances during calculations. They add together in series, and when parallel, the inverse is equal to the sum of the inverses of every individual impedance. But as I've mentioned before, the impedance will change with the frequency, making it extremely useful. In fact, this property is exactly what lets us use Radios and other wireless forms of communications, but that's FAR down the lane. But for now, impedances are over. I'll recommend a pizza, or maybe go watch a new episode of Shingeki no Kyojin or Boku no Hero Academia, have a bit of fun. This was a lot of work, but it's gonna get much better now onwards.
Complex Impedances, Voltages, and Currents
Weeellll, we've been through the easy part, so let's get started. I'll first introduce a useful concept called phasors, then we'll go on to the nitty gritty parts.
"Well then, what's a phasor?"
Uh, it's kinda hard to phrase, but simply put, if you have any functions that is a $sin()$ or $cos()$ based function, or can be represented in that form, is a function that can be represented as a phasor, and the phasor itself is simply a rotating line, with the magnitude equal to the maximum value of the function. I hope you're comfortable with trigonometry and geometry, 'cuz there's a lot of that in this section. Let's get started then, shall we?
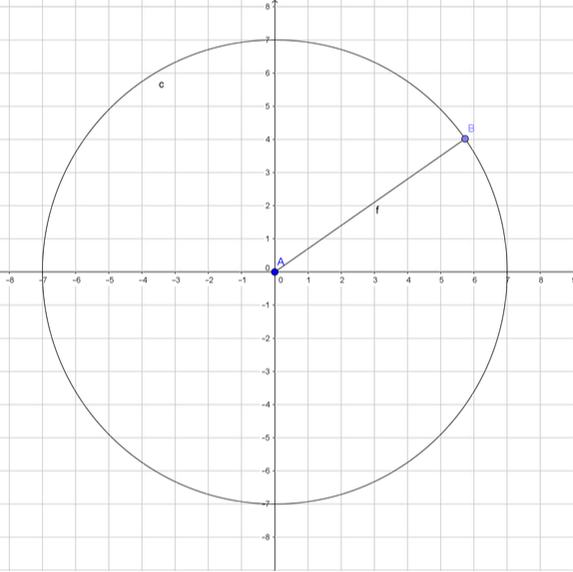
Let's understand how to represent a function as a phasor. Take something like, say - $f(x) = 7cos(5t)$.
Weeellll, we've been through the easy part, so let's get started. I'll first introduce a useful concept called phasors, then we'll go on to the nitty gritty parts.
"Well then, what's a phasor?"
Uh, it's kinda hard to phrase, but simply put, if you have any functions that is a $sin()$ or $cos()$ based function, or can be represented in that form, is a function that can be represented as a phasor, and the phasor itself is simply a rotating line, with the magnitude equal to the maximum value of the function. I hope you're comfortable with trigonometry and geometry, 'cuz there's a lot of that in this section. Let's get started then, shall we?
Let's understand how to represent a function as a phasor. Take something like, say - $f(x) = 7cos(5t)$.
So, it's a circle? No. That's only there to help you out a bit.
The actual phasor is the line $(A, B)$ (that's going to be our notation for a line between 2 points). And how does that work? Let's take a look at the x-axis.
But before that, keep in mind that the phase $5t$ is time dependent. This means it's going to at a rate of move 5 radians per second. So, the phasor, is effectively rotating.
If you remember your trigonometry, you should know that the projection of the phasor on the x-axis is $7cos(5t)$, finding that out will be your exercise. You should have noticed by now, that the function is represented, not by the phasor itself, but by the projection of it on the x-axis, or y-axis, depending on whether the function is $cos()$ or $sin()$ based. The phasor itself represents the phase information. You should also keep in mind that these phasors essentially behave as vectors. What does this mean? They behave as arrows pointing in a direction. It's not really a physical consequence. It's just that vectors are easy to manipulate, ie, it's a mathematical "bodge", sort of. They have their own properties, and are discussed in a previous primer.
The uses will be much easier to see in a practical example. But, for now, this is how a sinusoidal wave is represented.
In the end, what better way to learn something than do it yourself?
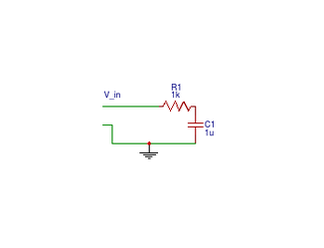
Let's take our good old RC circuit with an AC source instead of DC. The results are easy enough to calculate using calculus, but this is easier.
The actual phasor is the line $(A, B)$ (that's going to be our notation for a line between 2 points). And how does that work? Let's take a look at the x-axis.
But before that, keep in mind that the phase $5t$ is time dependent. This means it's going to at a rate of move 5 radians per second. So, the phasor, is effectively rotating.
If you remember your trigonometry, you should know that the projection of the phasor on the x-axis is $7cos(5t)$, finding that out will be your exercise. You should have noticed by now, that the function is represented, not by the phasor itself, but by the projection of it on the x-axis, or y-axis, depending on whether the function is $cos()$ or $sin()$ based. The phasor itself represents the phase information. You should also keep in mind that these phasors essentially behave as vectors. What does this mean? They behave as arrows pointing in a direction. It's not really a physical consequence. It's just that vectors are easy to manipulate, ie, it's a mathematical "bodge", sort of. They have their own properties, and are discussed in a previous primer.
The uses will be much easier to see in a practical example. But, for now, this is how a sinusoidal wave is represented.
In the end, what better way to learn something than do it yourself?
Let's take our good old RC circuit with an AC source instead of DC. The results are easy enough to calculate using calculus, but this is easier.
Let's a few notations out of the way first:
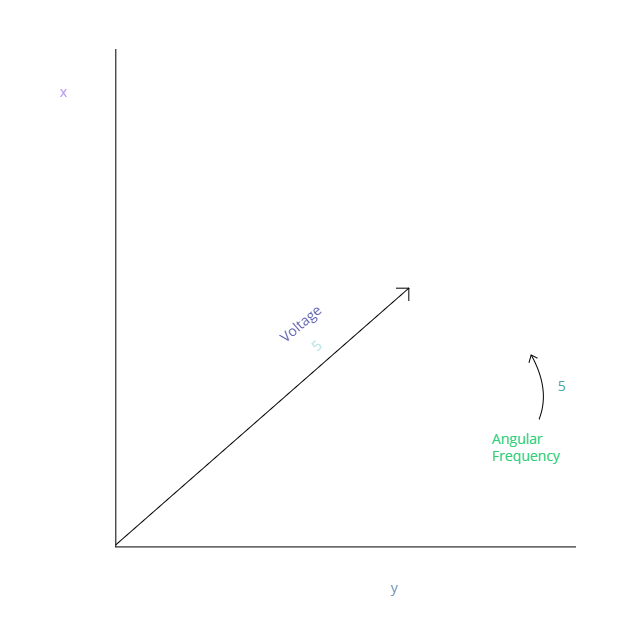
Also, $V_{in}(t) = 5sin(5t)$
Below is a picture of how $V_{in}$ can be represented in phasor form.
- $\vec V_{in}$ $\rightarrow$ The AC phasor
- $V_{in} \space \rightarrow$ The magnitude
Also, $V_{in}(t) = 5sin(5t)$
Below is a picture of how $V_{in}$ can be represented in phasor form.
Now, for the actual calculations, be extremely (OK, that's a bit extreme :3, but pay attention) observant. First we draw the usual axes. Then, we use KVL. Remember this fact VERY CLEARLY, KCL and KVL ONLY work with instantaneous voltages and currents, so you can't say $V_{in} = V_R + V_C$ (Labels are pretty damn obvious, so I won't bother with them for the rest of the tutorials), but you CAN say $V_{in}(t) = V_R(t) + V_C(t)$. The $(t)$ appended to the symbols imply that they aren't magnitudes, but instead functions (and thus the instantaneous value, for some time). And this relation is ALWAYS true.Technically speaking, you could take the long way and do this (there's high school level math here. Don't like it, skip it. But seriously, learn high school math if you wanna learn EE, like come on):
$$V_R(t) = i(t)R; \space V_C(t) = i(t - \frac{\pi}{2})X_C$$
Remember capacitors? If you do then you'll also remember that no the current through a capacitor was $\frac{\pi}{2}$ ahead of the voltage across it, so you can get something proportional to the voltage of the capacitor by subtracting $\frac{\pi}{2}$ from the phase of the current function. So, it's sort of basically usable in the equation above since the magnitude remains unchanged.
So,
$$V_{in}(t) = i(t)R + i(t - \frac{\pi}{2})X_C$$
We know that regardless what happens, if a signal source is sinusoidal in voltage, then the current will be sinusoidal with the same frequency, albeit with a phase shift. So it's reasonable to assume that -
$$i(t) = i_0cos(\omega t - \phi)$$
Substituting into the equation for $V_{in}(t)$
$$V_{in}(t) = Ri_0cos(\omega t - \phi) + X_C[i_0cos((\omega t - \phi) - \frac{\pi}{2})]$$
Here, I'd like to introduce other rules of trigonometry -
$$cos(\theta ) = cos(-\theta )$$
$$-sin(\theta ) = sin(-\theta )$$
$$sin(\theta) = cos(\frac{\pi}{2} - \theta)$$
$$cos(\theta ) = sin(\frac{\pi }{2} - \theta )$$
$$sin(\alpha + \beta ) = sin(\alpha )cos(\beta ) + sin(\beta )cos(\alpha )$$
$$cos(\alpha + \beta ) = cos(\alpha)cos(\beta) - sin(\alpha )sin(\beta )$$
Let's continue onward then
$$V_{in}(t) = Ri_0cos(\omega t - \phi) + X_C[i_0cos((\omega t - \phi) - \frac{\pi}{2})]$$
$$V_{in}(t) = Ri_0cos(\omega t - \phi) + X_Ci_0[cos(\frac{\pi}{2} - (\omega t - \phi))]$$
$$V_{in}(t) = Ri_0cos(\omega t - \phi) + X_Ci_0sin(\omega t - \phi)$$
$$V_{in}(t) = i_0 \left[ R cos(\omega t - \phi) + X_Csin(\omega t - \phi) \right]$$
$$V_{in}(t) = i_0\sqrt{R^2 + X_C^2}\left( \frac{R}{\sqrt{R^2 + X_C^2}}cos(\omega t - \phi) + \frac{X_C}{\sqrt{R^2 + X_C^2}}sin(\omega t -\phi)\right)$$
Here, we can define a few values. Let's say that $R$ and $X_C$ are the sides of a right angled triangle. If I were to pick an acute angle from the triangle, I can write it's trigonometric ratios now, and one thing you should keep in mind is that depending on the angle chosen,
we can get
$$sin(\alpha) = \frac{R}{\sqrt{R^2 + X_C^2}}$$
or
$$cos(\alpha) = \frac{R}{\sqrt{R^2 + X_C^2}}$$
I'll be going with the latter.
So, now the equation becomes -
$$V_{in}(t) = i_0\sqrt{R^2 + X_C^2}(cos(\alpha)cos(\omega t - \phi) + sin(\alpha)sin(\omega t - \phi))$$
Using one of the above stated identities,
$$V_{in}(t) = i_0\sqrt{R^2 + X_C^2}cos(\omega t - \phi - \alpha) = V_0cos(\omega t)$$
$$V_R(t) = i(t)R; \space V_C(t) = i(t - \frac{\pi}{2})X_C$$
Remember capacitors? If you do then you'll also remember that no the current through a capacitor was $\frac{\pi}{2}$ ahead of the voltage across it, so you can get something proportional to the voltage of the capacitor by subtracting $\frac{\pi}{2}$ from the phase of the current function. So, it's sort of basically usable in the equation above since the magnitude remains unchanged.
So,
$$V_{in}(t) = i(t)R + i(t - \frac{\pi}{2})X_C$$
We know that regardless what happens, if a signal source is sinusoidal in voltage, then the current will be sinusoidal with the same frequency, albeit with a phase shift. So it's reasonable to assume that -
$$i(t) = i_0cos(\omega t - \phi)$$
Substituting into the equation for $V_{in}(t)$
$$V_{in}(t) = Ri_0cos(\omega t - \phi) + X_C[i_0cos((\omega t - \phi) - \frac{\pi}{2})]$$
Here, I'd like to introduce other rules of trigonometry -
$$cos(\theta ) = cos(-\theta )$$
$$-sin(\theta ) = sin(-\theta )$$
$$sin(\theta) = cos(\frac{\pi}{2} - \theta)$$
$$cos(\theta ) = sin(\frac{\pi }{2} - \theta )$$
$$sin(\alpha + \beta ) = sin(\alpha )cos(\beta ) + sin(\beta )cos(\alpha )$$
$$cos(\alpha + \beta ) = cos(\alpha)cos(\beta) - sin(\alpha )sin(\beta )$$
Let's continue onward then
$$V_{in}(t) = Ri_0cos(\omega t - \phi) + X_C[i_0cos((\omega t - \phi) - \frac{\pi}{2})]$$
$$V_{in}(t) = Ri_0cos(\omega t - \phi) + X_Ci_0[cos(\frac{\pi}{2} - (\omega t - \phi))]$$
$$V_{in}(t) = Ri_0cos(\omega t - \phi) + X_Ci_0sin(\omega t - \phi)$$
$$V_{in}(t) = i_0 \left[ R cos(\omega t - \phi) + X_Csin(\omega t - \phi) \right]$$
$$V_{in}(t) = i_0\sqrt{R^2 + X_C^2}\left( \frac{R}{\sqrt{R^2 + X_C^2}}cos(\omega t - \phi) + \frac{X_C}{\sqrt{R^2 + X_C^2}}sin(\omega t -\phi)\right)$$
Here, we can define a few values. Let's say that $R$ and $X_C$ are the sides of a right angled triangle. If I were to pick an acute angle from the triangle, I can write it's trigonometric ratios now, and one thing you should keep in mind is that depending on the angle chosen,
we can get
$$sin(\alpha) = \frac{R}{\sqrt{R^2 + X_C^2}}$$
or
$$cos(\alpha) = \frac{R}{\sqrt{R^2 + X_C^2}}$$
I'll be going with the latter.
So, now the equation becomes -
$$V_{in}(t) = i_0\sqrt{R^2 + X_C^2}(cos(\alpha)cos(\omega t - \phi) + sin(\alpha)sin(\omega t - \phi))$$
Using one of the above stated identities,
$$V_{in}(t) = i_0\sqrt{R^2 + X_C^2}cos(\omega t - \phi - \alpha) = V_0cos(\omega t)$$
When comparing two elementary trigonometric functions, it's correct to assume that there is a one to one correspondence between the magnitudes and the ratio part of both functions. Essentially, that means-
While not quite correct, it's okay to say that-
$$\omega t -\alpha -\phi = \omega t$$
$$\phi = -\alpha$$
Keep this in mind for now. Next, the form of 2 should remind you of something.... yeah... real familiar... oh, wait,
$$V = IZ$$
- $cos(\omega t -\phi -\alpha) = cos(\omega t)$
- $V_0 = i_0\sqrt{R^2 + X_C^2}$
While not quite correct, it's okay to say that-
$$\omega t -\alpha -\phi = \omega t$$
$$\phi = -\alpha$$
Keep this in mind for now. Next, the form of 2 should remind you of something.... yeah... real familiar... oh, wait,
$$V = IZ$$
The above formula is true, and is also in a form comparable to 2, and by comparing, we can say that
$$Z = \sqrt{R^2 + X_C^2}$$
Let's modify this to make it useful anywhere. We define the reactance of a circuit as the sum of all inductive and capacitive reactances taking inductive reactances to be positive, and the other one to be negative. So, the reactance would be
$$X = \sum X_L - \sum X_C$$
Now, substitute it for X_C in the previous equation-
$$Z = \sqrt{R^2 + X^2}$$
This is one of the most important formulae you'll use in this field. LEARN IT. Don't worry if you don't get it. You'll get it a bit later down this page.
We know that $\phi$ is the phase difference between voltage and current.
Oh, btw remember how we defined $\alpha$? Yeah, $cos(\alpha) = \frac{R}{\sqrt{R^2 + X_C^2}}$, so, $\phi$ equals $arccos\left( \frac{R}{\sqrt{R^2 + X_C^2}}\right)$. I've neglected the minus sign, since it's in the end only an indicator of direction of rotation (positive corresponds to counterclockwise). Pretty cool coincidence, wouldn't you agree? The fact that the phase difference between voltage and current equals the arc-cosine of resistance over the impedance, somehow feels cool to me.
Now, for an easier way, we have phasors (or vectors). How long have we waited...(lol)(lol) (No, I'm not casul, I play DS, get out now)
Below is a picture of KVL applied to the different voltage phasors.
But before that (yes, I'm a tease, but you can gladly scroll down, and try to make sense of it) let's get some notation out of the way.
The last time $f(t)$ denoted the instantaneous value, and $f$ denoted the magnitude (for some $f$). Only the former experiences some change this around.
$$\vec f$$
represents the vector, and the instantaneous value is its projection on the x-axis (and vectors do comply with KCL and KVL. The math is a bit complicated, but I'll be happy to add that in case anybody wants it). For a simple intuitive answer on why, it's because adding vectors cause the same change in their projection as adding two $sin()$ or $cos()$ functions. Also, because of this, all the phase relations directly carry over (the voltage vector will be $\frac{\pi}{2}$ behind the current vector for a capacitor)
OK, now onto the circuit. According to KVL,
$$\vec V_{in} = \vec V_R + \vec V_C$$
$$Z = \sqrt{R^2 + X_C^2}$$
Let's modify this to make it useful anywhere. We define the reactance of a circuit as the sum of all inductive and capacitive reactances taking inductive reactances to be positive, and the other one to be negative. So, the reactance would be
$$X = \sum X_L - \sum X_C$$
Now, substitute it for X_C in the previous equation-
$$Z = \sqrt{R^2 + X^2}$$
This is one of the most important formulae you'll use in this field. LEARN IT. Don't worry if you don't get it. You'll get it a bit later down this page.
We know that $\phi$ is the phase difference between voltage and current.
Oh, btw remember how we defined $\alpha$? Yeah, $cos(\alpha) = \frac{R}{\sqrt{R^2 + X_C^2}}$, so, $\phi$ equals $arccos\left( \frac{R}{\sqrt{R^2 + X_C^2}}\right)$. I've neglected the minus sign, since it's in the end only an indicator of direction of rotation (positive corresponds to counterclockwise). Pretty cool coincidence, wouldn't you agree? The fact that the phase difference between voltage and current equals the arc-cosine of resistance over the impedance, somehow feels cool to me.
Now, for an easier way, we have phasors (or vectors). How long have we waited...(lol)(lol) (No, I'm not casul, I play DS, get out now)
Below is a picture of KVL applied to the different voltage phasors.
But before that (yes, I'm a tease, but you can gladly scroll down, and try to make sense of it) let's get some notation out of the way.
The last time $f(t)$ denoted the instantaneous value, and $f$ denoted the magnitude (for some $f$). Only the former experiences some change this around.
$$\vec f$$
represents the vector, and the instantaneous value is its projection on the x-axis (and vectors do comply with KCL and KVL. The math is a bit complicated, but I'll be happy to add that in case anybody wants it). For a simple intuitive answer on why, it's because adding vectors cause the same change in their projection as adding two $sin()$ or $cos()$ functions. Also, because of this, all the phase relations directly carry over (the voltage vector will be $\frac{\pi}{2}$ behind the current vector for a capacitor)
OK, now onto the circuit. According to KVL,
$$\vec V_{in} = \vec V_R + \vec V_C$$
What? $\vec i$? Why?
Because it's our reference. When we decode a single line of current (ie, in a mesh instead of loop by loop, you use line by line), we take the current to be at a rotation of 0 (Doesn't mean that the vectors aren't rotating, they damn well are, this is only for visualization, and convenience obviously). Now, let's see why each of the vectors are where they are. Let's start with $\vec V_R$, we know that $\vec V_R)$ has 0 phase difference relative to $\vec i$, so it points in the same direction. Also, $\vec V_C$ is $\frac{\pi}{2}$ behind (that means the angle would be subtracted from the phase of current, so it rotates clockwise by $\frac{\pi}{2}$). And, well we know from that what $\vec V_{in}$ is. Using basic Pythagoras' theorem, we can say that $V_{in}^2 = V_R^2 + V_C^2$ (You can, and should derive it always from Vector addition, since it's not going to be a $\frac{\pi}{2} phase difference all the time$), and we can simply calculate the values of $V_R$ and $V_C$. Borrowing from previous calculations,
$$V_{in}^2 = i^2\left(R^2 + X_C^2\right)$$
$$V_{in} = iZ$$
Let's be a bit clever. Let's make a vector diagram of the impedances (not phasors because they don't rotate). How do we do it? Well, since the magnitude of the impedance is the root of the sum of squares of the resistance and the reactance, we can consider two axes, one resistive, the other reactive, this way, a vectors magnitude will be the root of the sum of the squares of the resistance and reactance. Which one is which is something completely left to us, so let's choose the convention - resistance is represented by the horizontal axis, and reactance by the vertical. So, in the end we get this -
Because it's our reference. When we decode a single line of current (ie, in a mesh instead of loop by loop, you use line by line), we take the current to be at a rotation of 0 (Doesn't mean that the vectors aren't rotating, they damn well are, this is only for visualization, and convenience obviously). Now, let's see why each of the vectors are where they are. Let's start with $\vec V_R$, we know that $\vec V_R)$ has 0 phase difference relative to $\vec i$, so it points in the same direction. Also, $\vec V_C$ is $\frac{\pi}{2}$ behind (that means the angle would be subtracted from the phase of current, so it rotates clockwise by $\frac{\pi}{2}$). And, well we know from that what $\vec V_{in}$ is. Using basic Pythagoras' theorem, we can say that $V_{in}^2 = V_R^2 + V_C^2$ (You can, and should derive it always from Vector addition, since it's not going to be a $\frac{\pi}{2} phase difference all the time$), and we can simply calculate the values of $V_R$ and $V_C$. Borrowing from previous calculations,
$$V_{in}^2 = i^2\left(R^2 + X_C^2\right)$$
$$V_{in} = iZ$$
Let's be a bit clever. Let's make a vector diagram of the impedances (not phasors because they don't rotate). How do we do it? Well, since the magnitude of the impedance is the root of the sum of squares of the resistance and the reactance, we can consider two axes, one resistive, the other reactive, this way, a vectors magnitude will be the root of the sum of the squares of the resistance and reactance. Which one is which is something completely left to us, so let's choose the convention - resistance is represented by the horizontal axis, and reactance by the vertical. So, in the end we get this -
Another way to get this diagram would be to divide all the voltage phasors in the voltage diagram by $i$, and you'll get a diagram identical to this. That's also why $\phi$ carries over here as well. From here, again, one can derive the formula relating the impedance and the phase difference. You don't really need to use this to solve your questions, in fact, it's easier to use the above diagram. But there's something you can learn from this. Remember how we defined the reactance of a circuit? The convention we took there can be explained here. Because, if you were to represent the voltage across an inductor, because the current through it is always $\frac{\pi}{2}$ BEHIND the voltage, the voltage would be vertically upwards, and if we made an impedance diagram from that, it can be clearly seen that the vector for inductive impedance would be pointing vertically upwards , which is the positive direction according to conventions. So, $X$ being defined as $\sum X_L - \sum X_C$ makes it easy as we can replace two or more vectors with one (since they are parallel or anti-parallel, you can simply add them like normal integers) and calculate Z with ease. There's also another reason for its existence, but we'll keep that for the next section. While this is an easier method for solving circuits, this becomes as complex and tedious as trigonometric manipulation if not more for more complicated meshes. Which is why the most used method is complex analysis. We basically exploit the fact that complex numbers can be represented as vectors, and instead represent phasors AS complex numbers.
Let's see what I mean -
$$\vec A = a \hat x + b \hat y$$
$$Z = a + ib$$
$Z$ behaves like $\vec A$ for all practical purposes. And here's what makes complex analysis useful. Remember Euler's theorem? Using that we can define $\vec A$ as an exponential function, and this is great because multiplication leads to a simple addition or subtraction in the exponent of $e$.
With that aside, as usual, let's fix our notation -
$\vec A$ will be now represented as $\Bbb A$, when using complex analysis.
Also, $j = \sqrt{-1}$ instead of $i$ because $i$ is frequently used to represent current in EE.
Let's try representing the voltage as a complex number.
$$\vec V_{in} = V_0(cos(\omega t) \hat x + sin(\omega t) \hat y)$$
So, following the previous example,
$$\Bbb V_{in} = V_0(cos(\omega t) + j \cdot sin(\omega t))$$
And here, we use Euler's formula-
$$cos(\omega t) + j\cdot sin(\omega t) = e^{j\omega t}$$
$$\implies V_{in} = V_0e^{j\omega t}$$
We got a complex number, remember that. By our conventions, it's the x-axis projection that represents the function, and to get that for a complex number, we use the $Re()$ operator (if y-axis is what you're using use $Im()$).
So, $$V_{in}(t) = Re(V_0\cdot e^{j\omega t}$$
Ans that's true for every current and voltage, just follow one convention. Or you'll experience hell. Your wish.
Another thing to note is that interestingly if we apply the operators to $\Bbb Z$, we get $R$ from $Re()$ and $X$ from $Im()$.
Now, let's solve that stupid problem completely. Let's calculate the total impedance -
$$\Bbb Z = R + jX_C$$
$$X_C = -\frac{1}{\omega C_1} = -\frac{1}{5 \cdot 10^{-6}} = -2\cdot 10^5$$
$$\implies \Bbb Z = 10^3 - j\cdot 2\cdot 10^5$$
We want $\Bbb Z$ in exponential form. So, like with the calculations during the trigonometric manipulation, we consider the two components as sides of a right angled triangle, this means, when divided by the hypotenuse, they represent the $sin()$ and $cos()$ functions' values at that angle. To do that, we can multiply and divide by the hypotenuse, which is $Z$ (Find out why yourself. Once you do this, solving problems on yourself should be a cinch), so we get-
$$\Bbb Z = Z(R/Z - iX_C/Z)$$
$$\Bbb Z = Z(cos(-\phi) + isin(-\phi))$$
$$\Bbb Z = Z\cdot e^{-j\phi}$$
$$\Bbb V_{in} = V_0\cdot e^{j\omega t}$$
$$\Bbb i = \Bbb{\frac{V_{in}}{Z}} = \frac{V_0}{Z}\cdot e^{j\omega t + \phi}$$
$$i(t) = Re(\Bbb i) = \frac{V_0}{Z}\cdot cos(\omega t + \phi)$$
$$i(t) = \frac{5}{200000}\cdot cos(\omega t + \phi)$$
$$\phi = arccos(Z) = 1.567 radians$$
$$\implies i(t) = \frac{1}{40000}\cdot cos(5t + 1.567)$$
And voila! There it is.
That's all folks. That is all. In the next few tutorials, we'll be analyzing a few useful circuits, visit again in a day or two. This is probably going to take a lot of time to understand properly. Especially the complex numbers part. Don't worry about that. Once we start analyzing circuits, that shouldn't be a problem.
I'll be using phasors and complex numbers for simpler circuits, and then we'll gradually shift over to complex numbers only after 2 or 3 circuits.
Let's see what I mean -
$$\vec A = a \hat x + b \hat y$$
$$Z = a + ib$$
$Z$ behaves like $\vec A$ for all practical purposes. And here's what makes complex analysis useful. Remember Euler's theorem? Using that we can define $\vec A$ as an exponential function, and this is great because multiplication leads to a simple addition or subtraction in the exponent of $e$.
With that aside, as usual, let's fix our notation -
$\vec A$ will be now represented as $\Bbb A$, when using complex analysis.
Also, $j = \sqrt{-1}$ instead of $i$ because $i$ is frequently used to represent current in EE.
Let's try representing the voltage as a complex number.
$$\vec V_{in} = V_0(cos(\omega t) \hat x + sin(\omega t) \hat y)$$
So, following the previous example,
$$\Bbb V_{in} = V_0(cos(\omega t) + j \cdot sin(\omega t))$$
And here, we use Euler's formula-
$$cos(\omega t) + j\cdot sin(\omega t) = e^{j\omega t}$$
$$\implies V_{in} = V_0e^{j\omega t}$$
We got a complex number, remember that. By our conventions, it's the x-axis projection that represents the function, and to get that for a complex number, we use the $Re()$ operator (if y-axis is what you're using use $Im()$).
So, $$V_{in}(t) = Re(V_0\cdot e^{j\omega t}$$
Ans that's true for every current and voltage, just follow one convention. Or you'll experience hell. Your wish.
Another thing to note is that interestingly if we apply the operators to $\Bbb Z$, we get $R$ from $Re()$ and $X$ from $Im()$.
Now, let's solve that stupid problem completely. Let's calculate the total impedance -
$$\Bbb Z = R + jX_C$$
$$X_C = -\frac{1}{\omega C_1} = -\frac{1}{5 \cdot 10^{-6}} = -2\cdot 10^5$$
$$\implies \Bbb Z = 10^3 - j\cdot 2\cdot 10^5$$
We want $\Bbb Z$ in exponential form. So, like with the calculations during the trigonometric manipulation, we consider the two components as sides of a right angled triangle, this means, when divided by the hypotenuse, they represent the $sin()$ and $cos()$ functions' values at that angle. To do that, we can multiply and divide by the hypotenuse, which is $Z$ (Find out why yourself. Once you do this, solving problems on yourself should be a cinch), so we get-
$$\Bbb Z = Z(R/Z - iX_C/Z)$$
$$\Bbb Z = Z(cos(-\phi) + isin(-\phi))$$
$$\Bbb Z = Z\cdot e^{-j\phi}$$
$$\Bbb V_{in} = V_0\cdot e^{j\omega t}$$
$$\Bbb i = \Bbb{\frac{V_{in}}{Z}} = \frac{V_0}{Z}\cdot e^{j\omega t + \phi}$$
$$i(t) = Re(\Bbb i) = \frac{V_0}{Z}\cdot cos(\omega t + \phi)$$
$$i(t) = \frac{5}{200000}\cdot cos(\omega t + \phi)$$
$$\phi = arccos(Z) = 1.567 radians$$
$$\implies i(t) = \frac{1}{40000}\cdot cos(5t + 1.567)$$
And voila! There it is.
That's all folks. That is all. In the next few tutorials, we'll be analyzing a few useful circuits, visit again in a day or two. This is probably going to take a lot of time to understand properly. Especially the complex numbers part. Don't worry about that. Once we start analyzing circuits, that shouldn't be a problem.
I'll be using phasors and complex numbers for simpler circuits, and then we'll gradually shift over to complex numbers only after 2 or 3 circuits.