Complex Numbers
Prerequisites:
- Knowledge of Trigonometry
As you've seen in my capacitor tutorial, math related to it (and inductors, which we will learn a bit later) can get "hairy". And by hairy, I mean something like a gorilla. So, to avoid that kinda "hairiness", physicists, being the lazy guys they are, bodged up a way to easily calculate everything using complex numbers, and our original laws. But to learn that, you might wanna learn about complex numbers. Obviously, if you know the relation $e^{{\pi}i} + 1 = 0$, you'll want to skip this.
So what exactly are complex numbers? Some kinda Voodoo magic? Nah. Are they hard? If you ever found arithmetic hard, then yes, if not, then no. What are they though?
Well, Complex numbers are quite simply a "complex" of real and imaginary numbers. Clearing the concept of imaginary numbers is important here. Let's say we have an equation -
$$x^2 = a$$
What's x? That's easy -
$$x = ^+_-\sqrt{a}$$
Since if we have any numer $a$ or $-a$, $a^2 = (-a)^2$, since the negative sign cancles out.
That's all great and awesome, but from above it's quite easy to see that the square of any number is always positive -
$$a = b^2, \qquad \qquad a \in \Bbb{W}, b \in \Bbb{R}$$
Don't worry if you're not sure what "$\in$" or "$\Bbb{R}, \Bbb{W}$" means, all that it means is that in the above equation, $a$ is a number of the "set" (a collection of "something", numbers in this case) of whole numbers (numbers you can count- $\Bbb{W} = \{0, 1, 2, 3...\}$) and similarly, $b$ belongs to the set of real numbers (numbers on the number line).
Back on track, what IF $a$ wasn't positive, what if it was negative? Something a bit easier would be-
$$x^2 = -1$$
$$\Rightarrow x = \sqrt{-1}$$
Hey..., wait a minute, there's no possible way a number could be a square root of a negative number..
Why? Since no matter what number you take that's on the number line (what's called real numbers), the square of it is ALWAYS positive.... So, we simply say, let $\sqrt{-1} = i$.
Doesn't that mean we don't know the value of $i$? Yes, we don't.. That's why it's called "imaginary", it doesn't EXIST on the number line...
So let's define an imaginary number-
$$\omega = ni \qquad \qquad n \in \Bbb{R}$$
Another thing you should know is that since we don't KNOW what $i$ is, we can't say if $3i > 2i$, we simply don't know about it.
Let's say, we want to know what $\sqrt{-5}$ is. We can write it in terms of $i$ - $\sqrt{5} \times i$ Another thing you should keep in mind is that multipkication of square roots is only defined if atleast one of the two multiplicands (fancy word for th two terms you multiply together) is a proper real number. As for those involving $i$'s, we use the following series-
$$i^{4n} = 1, \; i^{4n + 1} = i,\; i^{4n + 2} = -1,\; i^{4n + 3} = -i \qquad n \in \Bbb{I}$$
Btw, $\Bbb{I} = \{..... -3, -2, -1, 0, 1, 2, 3 .....\}$, and they're called integers.
Just in case you haven't realized, the series I gave you is sort of a mathematical bodge.. It simply solves many "paradoxes"...
Now we can finally get into complex numbers. As I wrote above, a complex number is literally a "complex" (mixture) of real and imaginary numbers. Any complex number is going to be denoted commonly by $Z$ or $\omega$. Also, the set of complex numbers is written as $\Bbb{Z}$.
So, basically a complex number is any number of the form-
$$Z = a + ib \qquad a, b \in \Bbb{R}$$
Now let's switch over to a much better graphical representation. I'm pretty sure everybody knows about the euclidean plane (Another fancy mathematical term for a plane that has x and y axes, mathematicians... you can never stop them.. ;-P), when you replace the y-axis with an imaginary axis (basically multiply every number on the y axis with $i$, and you get the "imaginary axis".. I kinda wish that they'd atleast choose cooler names...), you get the "argent plane"... Yeah....
Back on track, let's say we have this number - $4 + 3i$, we'll represent it like the picture below-
So what exactly are complex numbers? Some kinda Voodoo magic? Nah. Are they hard? If you ever found arithmetic hard, then yes, if not, then no. What are they though?
Well, Complex numbers are quite simply a "complex" of real and imaginary numbers. Clearing the concept of imaginary numbers is important here. Let's say we have an equation -
$$x^2 = a$$
What's x? That's easy -
$$x = ^+_-\sqrt{a}$$
Since if we have any numer $a$ or $-a$, $a^2 = (-a)^2$, since the negative sign cancles out.
That's all great and awesome, but from above it's quite easy to see that the square of any number is always positive -
$$a = b^2, \qquad \qquad a \in \Bbb{W}, b \in \Bbb{R}$$
Don't worry if you're not sure what "$\in$" or "$\Bbb{R}, \Bbb{W}$" means, all that it means is that in the above equation, $a$ is a number of the "set" (a collection of "something", numbers in this case) of whole numbers (numbers you can count- $\Bbb{W} = \{0, 1, 2, 3...\}$) and similarly, $b$ belongs to the set of real numbers (numbers on the number line).
Back on track, what IF $a$ wasn't positive, what if it was negative? Something a bit easier would be-
$$x^2 = -1$$
$$\Rightarrow x = \sqrt{-1}$$
Hey..., wait a minute, there's no possible way a number could be a square root of a negative number..
Why? Since no matter what number you take that's on the number line (what's called real numbers), the square of it is ALWAYS positive.... So, we simply say, let $\sqrt{-1} = i$.
Doesn't that mean we don't know the value of $i$? Yes, we don't.. That's why it's called "imaginary", it doesn't EXIST on the number line...
So let's define an imaginary number-
$$\omega = ni \qquad \qquad n \in \Bbb{R}$$
Another thing you should know is that since we don't KNOW what $i$ is, we can't say if $3i > 2i$, we simply don't know about it.
Let's say, we want to know what $\sqrt{-5}$ is. We can write it in terms of $i$ - $\sqrt{5} \times i$ Another thing you should keep in mind is that multipkication of square roots is only defined if atleast one of the two multiplicands (fancy word for th two terms you multiply together) is a proper real number. As for those involving $i$'s, we use the following series-
$$i^{4n} = 1, \; i^{4n + 1} = i,\; i^{4n + 2} = -1,\; i^{4n + 3} = -i \qquad n \in \Bbb{I}$$
Btw, $\Bbb{I} = \{..... -3, -2, -1, 0, 1, 2, 3 .....\}$, and they're called integers.
Just in case you haven't realized, the series I gave you is sort of a mathematical bodge.. It simply solves many "paradoxes"...
Now we can finally get into complex numbers. As I wrote above, a complex number is literally a "complex" (mixture) of real and imaginary numbers. Any complex number is going to be denoted commonly by $Z$ or $\omega$. Also, the set of complex numbers is written as $\Bbb{Z}$.
So, basically a complex number is any number of the form-
$$Z = a + ib \qquad a, b \in \Bbb{R}$$
Now let's switch over to a much better graphical representation. I'm pretty sure everybody knows about the euclidean plane (Another fancy mathematical term for a plane that has x and y axes, mathematicians... you can never stop them.. ;-P), when you replace the y-axis with an imaginary axis (basically multiply every number on the y axis with $i$, and you get the "imaginary axis".. I kinda wish that they'd atleast choose cooler names...), you get the "argent plane"... Yeah....
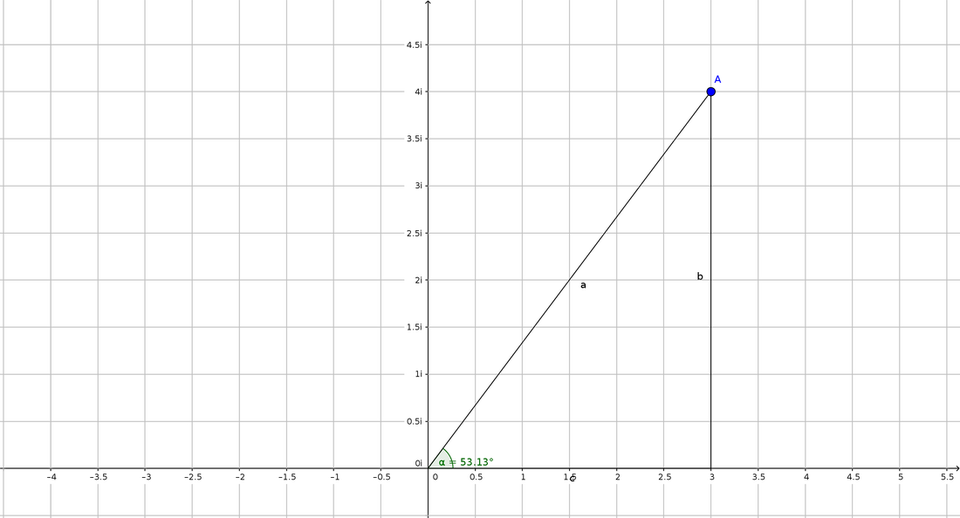
Back on track, let's say we have this number - $4 + 3i$, we'll represent it like the picture below-
There's another way of representing the same number (which eases calculation, and you'll know why later down the road).
What if we took the length of $a$, and then represented it in terms of trigonometric ratios? Seems complex, but really easy-
First we need the length of $a$, and for that we use our good old friend the pythgoras theorem
$$a^2 = b^2 + c^2$$
$$a^2 = 16 + 9$$
$$a^2 = 25 \Rightarrow a = 5$$
You might have noticed that I didn't use $i$ in the calculation, that's because I want the length of the line segment $a$, I'm not computing complex numbers here, simple geometry.
Now if you remember what you learnt in the last tutorial, we know that-
$$sin(\alpha) = \frac{b}{a}$$
which means we can say that
$$ b = asin(\alpha)$$
You might also remember that-
$$cos(\alpha) = \frac{c}{a}$$
So,
$$c = acos{\alpha}$$
And since our number is $c + bi$, we can represent it as-
$$acos(\alpha) + aisin(\alpha)$$
Why is this form not more complex and easier? Well, this is why-
$$e^{i\alpha} = cos(\alpha) + isin(\alpha)$$
So, we can simply represent our number as
$$5e^{i\alpha}$$
for obvious reasons.
What's so great about it? Well, if we multiply different complex numbers together (whcih is going to be quite common), we'll need to do long expansions, or we could be awesome and use thae above form, doing so allows us to simply add the exponents.
Another thing you should know is that $Re(Z)$ means the real part of the complex number $Z$, and $Im(Z)$ is the imaginary part.
We've finally finished the math part of this series. Wohoo. We can finally get into the exciting stuff. ^^
What if we took the length of $a$, and then represented it in terms of trigonometric ratios? Seems complex, but really easy-
First we need the length of $a$, and for that we use our good old friend the pythgoras theorem
$$a^2 = b^2 + c^2$$
$$a^2 = 16 + 9$$
$$a^2 = 25 \Rightarrow a = 5$$
You might have noticed that I didn't use $i$ in the calculation, that's because I want the length of the line segment $a$, I'm not computing complex numbers here, simple geometry.
Now if you remember what you learnt in the last tutorial, we know that-
$$sin(\alpha) = \frac{b}{a}$$
which means we can say that
$$ b = asin(\alpha)$$
You might also remember that-
$$cos(\alpha) = \frac{c}{a}$$
So,
$$c = acos{\alpha}$$
And since our number is $c + bi$, we can represent it as-
$$acos(\alpha) + aisin(\alpha)$$
Why is this form not more complex and easier? Well, this is why-
$$e^{i\alpha} = cos(\alpha) + isin(\alpha)$$
So, we can simply represent our number as
$$5e^{i\alpha}$$
for obvious reasons.
What's so great about it? Well, if we multiply different complex numbers together (whcih is going to be quite common), we'll need to do long expansions, or we could be awesome and use thae above form, doing so allows us to simply add the exponents.
Another thing you should know is that $Re(Z)$ means the real part of the complex number $Z$, and $Im(Z)$ is the imaginary part.
We've finally finished the math part of this series. Wohoo. We can finally get into the exciting stuff. ^^