Ohm's Law And Kirchoff's Laws And The Resistor
Prerequisites:
Ohm's Law:
The MOST important thing you're going to learn is called Ohm's Law. Yes it's a bit of math, but c'mon, it's 6th grade stuff...
Even though it's the most important law you're going to learn, it's really easy-
$$V = IR$$
"That's it?" Yes. That's it . All it really means is that the voltage drop (the voltage across the two terminals of a component) equals the product of the current flowing through it and the resistance of the component.
Resistances and Resistors:
Resistance, is a new term, so let me explain. It means what it's named. It's the "resistance" of a component against the flow of current.
Every component has a resistance (to be exact, impedance, but let's leave that for now). It's usually constant for certain components, but there are componenets that don't have a constant resistance. In real life, you'll also encounter parasitic resistance, which means that every single piece of conductor that your current flows through will resist the flow of current. Yes that means that a copper wire provides resistance. But resistances can be really useful. And there are certain devices called resistors that exploit this.
Resistors by the way are some of the most useful components ever. There will be literally no circuits without a resistor. And a resistor is a component with constant resistance. You might not see the use of this component immediately until you notice that you can use this to limit current. Let's say that there's a lamp, if you don't limit the current to it, you're going to burn it out because of the current you pump through it, also, it'd be really wasteful, you'd be wasting a lot of energy which is a no-no for battery applications, so you can use a resistor to limit the current through it. There really isn't much more to resistors than that. So be happy, because you just learnt you first component.
Kirchoff's Voltage and Current Laws:
This is another thing you wanna know if you wanna make your life easier when analyzing circuits, and trust me, this is a god send when it comes to that.
Let's start of with the current law:
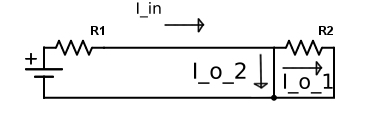
Kirchoff's current law basically tells us that if there is a junction (a place where two or more wires meet), then the current going into the junction equals the current coming out of it. Pretty simple huh? But it's really useful.
- A bit of 6th grade math
Ohm's Law:
The MOST important thing you're going to learn is called Ohm's Law. Yes it's a bit of math, but c'mon, it's 6th grade stuff...
Even though it's the most important law you're going to learn, it's really easy-
$$V = IR$$
"That's it?" Yes. That's it . All it really means is that the voltage drop (the voltage across the two terminals of a component) equals the product of the current flowing through it and the resistance of the component.
Resistances and Resistors:
Resistance, is a new term, so let me explain. It means what it's named. It's the "resistance" of a component against the flow of current.
Every component has a resistance (to be exact, impedance, but let's leave that for now). It's usually constant for certain components, but there are componenets that don't have a constant resistance. In real life, you'll also encounter parasitic resistance, which means that every single piece of conductor that your current flows through will resist the flow of current. Yes that means that a copper wire provides resistance. But resistances can be really useful. And there are certain devices called resistors that exploit this.
Resistors by the way are some of the most useful components ever. There will be literally no circuits without a resistor. And a resistor is a component with constant resistance. You might not see the use of this component immediately until you notice that you can use this to limit current. Let's say that there's a lamp, if you don't limit the current to it, you're going to burn it out because of the current you pump through it, also, it'd be really wasteful, you'd be wasting a lot of energy which is a no-no for battery applications, so you can use a resistor to limit the current through it. There really isn't much more to resistors than that. So be happy, because you just learnt you first component.
Kirchoff's Voltage and Current Laws:
This is another thing you wanna know if you wanna make your life easier when analyzing circuits, and trust me, this is a god send when it comes to that.
Let's start of with the current law:
Kirchoff's current law basically tells us that if there is a junction (a place where two or more wires meet), then the current going into the junction equals the current coming out of it. Pretty simple huh? But it's really useful.
You should be able to tell by now that $I_{in} = I_{o_1} + I_{o_2}$. This might not seem like much, but later down this article, I'll show you why it's so great.
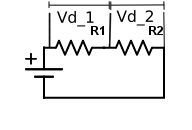
Let's talk about the voltage law, shall we? It's quite simple, since energy in a circuit is constant, we can say that the energy gained by the electrons is lost somehow, so we can say that the voltage, which is the energy per unit charge is in a loop, zero. So, if you sum up every voltage drop, you'll get zero. Again, a diagram should clarify things. And that's all the reading you need to do.
Below,
$$V_{bat} = V_{d_1} + V_{d_2}$$
Let's talk about the voltage law, shall we? It's quite simple, since energy in a circuit is constant, we can say that the energy gained by the electrons is lost somehow, so we can say that the voltage, which is the energy per unit charge is in a loop, zero. So, if you sum up every voltage drop, you'll get zero. Again, a diagram should clarify things. And that's all the reading you need to do.
Below,
$$V_{bat} = V_{d_1} + V_{d_2}$$
In Practice
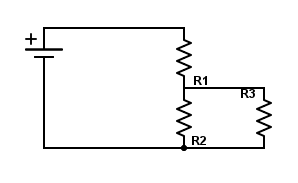
Let's derive the equations for a voltage divider. A really simple circuit shown below:
Here R3 is your load, so you can ignore it, to simplify our calculations. There's gonna be a bit of (6th grade) math, so gear up.
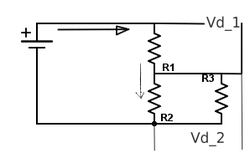
The Voltage divider by the way can provide any voltage between Vcc (The positive voltage of you power supply/battery), so it's really useful in many circuits. So let's see the schematic again but this time with currents and Voltage drops labelled:
The Voltage divider by the way can provide any voltage between Vcc (The positive voltage of you power supply/battery), so it's really useful in many circuits. So let's see the schematic again but this time with currents and Voltage drops labelled:
There's only one current flowing through the circuit (as I said, ignore the load R3), so let's call it I. There are 2 voltage drops - $V_{d_1}$ and $V_{d_2}$.
We know that $V_{d_1} = R_1 \times I$, and similarly, $V_{d_2} = R_2 \times I$ by Ohm's law. We also know by KVL that the voltage produced by the power supply
$$V_{in} = V_{d_1} + V_{d_2}$$
$$V_{in} = \left(R_1 + R_2 \right) \times I$$
$$\frac{V_{in}}{\left(R_1 + R_2\right)} = I$$
Since
$$V_{out} = V_{d_2}$$ ($V_{out}$ = the voltage across the load resistor)
and
$$\frac{V_{in}}{\left(R_1 + R_2\right)} = \frac{V_{d_2}}{R_2}$$
$$V_{out} = \frac{(V_{in} \times R_2)}{\left(R_1 + R_2\right)}$$
And there you have it, a great way of making a voltage source, and one that you'll use often. For example, if we have a Vin of 10V, and we want a 5V voltage, we could use any two resistors of the same value, and we'll get 5V according to the formula above.
And you've mastered everything there is to master about resistors.
We know that $V_{d_1} = R_1 \times I$, and similarly, $V_{d_2} = R_2 \times I$ by Ohm's law. We also know by KVL that the voltage produced by the power supply
$$V_{in} = V_{d_1} + V_{d_2}$$
$$V_{in} = \left(R_1 + R_2 \right) \times I$$
$$\frac{V_{in}}{\left(R_1 + R_2\right)} = I$$
Since
$$V_{out} = V_{d_2}$$ ($V_{out}$ = the voltage across the load resistor)
and
$$\frac{V_{in}}{\left(R_1 + R_2\right)} = \frac{V_{d_2}}{R_2}$$
$$V_{out} = \frac{(V_{in} \times R_2)}{\left(R_1 + R_2\right)}$$
And there you have it, a great way of making a voltage source, and one that you'll use often. For example, if we have a Vin of 10V, and we want a 5V voltage, we could use any two resistors of the same value, and we'll get 5V according to the formula above.
And you've mastered everything there is to master about resistors.